Unveiling the puzzle of mass at the speed of light
ไขปริศนามวล ณ ความเร็วแสง
"In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual(1632)".(Galileo Galilei 1564–1642)
มวลอนันต์มาจากไหน?
ไขปริศนามวล ณ ความเร็วแสง
"In questions of science, the authority of a thousand is not worth the humble reasoning of a single individual(1632)".(Galileo Galilei 1564–1642)
มวลอนันต์มาจากไหน?
แนวคิดเรื่องมวล มีมานับแต่ยุคเซอร์นิวตัน โดยเชื่อว่ามวลจะมีค่าคงที่-ไม่เปลี่ยนแปลง( invariant mass ) ซึ่งมักถูกเรียกอีกชื่อว่า มวลนิ่ง( rest mass )สัญลักษณ์ m0 โดยมวลในฟิสิกส์ยุคเริ่มแรก ถูกกำหนดให้เป็นคุณสมบัติของวัตถุที่สัมพันธ์กับขนาดของแรง เช่น ปรากฏในสมการ F=ma เป็นต้น
ขณะเดียวกันทฤษฎีมวลไ่ม่คงที่ หรือมวลสัมพัทธ์( Relativistic mass ) ซึ่งถูกนิยามครั้งแรกในปี 1912 โดย Richard C. Tolman โดยเขากล่าวว่า "the expression m0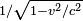 is best suited for the mass of a moving body."
is best suited for the mass of a moving body."
จากนั้น แนวคิดเรื่องมวลสัมพัทธ์กลายเป็นที่รู้จัก และใช้กันอย่างกว้างขวางในแวงวงฟิสิกส์ ดังปรากฏในตำราฟิสิกส์เชิงสัมพัทธภาพนับแต่ทศวรรษ 1920s เป็นต้นมา
โดยกล่าวถึงมวลสัมพัทธ์ในกรณีผู้สังเกตการณ์อยู่ในกรอบที่ไม่มีอัตราเร่ง ทฤษฎีพยากรณ์ว่าเขาวัดความยาวของวัตถุหดสั้นลงเมื่อวัตถุเคลื่อนที่ด้วยความเร็วใกล้แสง และเวลาของวัตถุในกรอบการเคลื่อนที่นั้นจะหดสั้นลงและกลายเป็นศูนย์เมื่อวัตถุนั้นเคลื่อนที่ด้วยความเร็วแสง ขณะเดียวกันมวลสัมพัทธ์ถูกตีความว่ามีค่าเป็น"อนันต์" คือ มหาศาล เมื่อวัตถุนั้นเคลื่อนที่ด้วยความเร็วแสง c และสรุปต่อไปว่า ไม่มีวัตถุใดเคลื่อนที่ด้วยความเร็วแสงได้ ความเร็วแสงเป็นขีดจำกัดความเร็วของวัตถุ หรือ ความเร็วแสงเป็นความเร็วต้องห้าม เป็นต้น
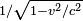 is best suited for the mass of a moving body."
is best suited for the mass of a moving body."จากนั้น แนวคิดเรื่องมวลสัมพัทธ์กลายเป็นที่รู้จัก และใช้กันอย่างกว้างขวางในแวงวงฟิสิกส์ ดังปรากฏในตำราฟิสิกส์เชิงสัมพัทธภาพนับแต่ทศวรรษ 1920s เป็นต้นมา
โดยกล่าวถึงมวลสัมพัทธ์ในกรณีผู้สังเกตการณ์อยู่ในกรอบที่ไม่มีอัตราเร่ง ทฤษฎีพยากรณ์ว่าเขาวัดความยาวของวัตถุหดสั้นลงเมื่อวัตถุเคลื่อนที่ด้วยความเร็วใกล้แสง และเวลาของวัตถุในกรอบการเคลื่อนที่นั้นจะหดสั้นลงและกลายเป็นศูนย์เมื่อวัตถุนั้นเคลื่อนที่ด้วยความเร็วแสง ขณะเดียวกันมวลสัมพัทธ์ถูกตีความว่ามีค่าเป็น"อนันต์" คือ มหาศาล เมื่อวัตถุนั้นเคลื่อนที่ด้วยความเร็วแสง c และสรุปต่อไปว่า ไม่มีวัตถุใดเคลื่อนที่ด้วยความเร็วแสงได้ ความเร็วแสงเป็นขีดจำกัดความเร็วของวัตถุ หรือ ความเร็วแสงเป็นความเร็วต้องห้าม เป็นต้น
แนวคิดทฤษฎีดังกล่าวอ้างจากทฤษฎีที่ว่า มวลสัมพัทธ์ สัญลักษณ์ mจะมีค่าที่ขึ้นอยู่กับความเร็วของวัตถุตามสมการนี้คือ
m=γm0
กรณีวัตถุเคลื่อนที่ด้วยความเร็วแสง แทนค่า v=c จะได้ว่า m=m0/0
อาศัยการตีความทางคณิตศาสตร์ จะได้คำตอบว่า m= infinity
ดังนั้น นับแต่ทศวรรษ 1920s เป็นต้นมา นักฟิสิกส์ทั่วโลกยอมรับว่า มวลสัมพัทธ์เพิ่มขึ้นตามความเร็ว และมวลเป็นอนันต์เมื่อ v=c (ดูกราฟฟิกเพิ่มเติม)
ขณะเดียวกันปัญหาเรื่องมวลสัมพัทธ์ ได้กลายเป็นหัวข้อใหญ่ของการอภิปรายทางฟิสิกส์อีกครั้งในปี ค.ศ.1989 เมื่อ Lev Okun นักฟิสิกส์ชาวรัสเซีย ได้เขียนบทความ"The Concept of Mass" ในวารสาร Physics Today ในปี 1989 โดยเขาเห็นว่าแนวคิดมวลสัมพัทธ์ไม่จะควรสอนกันอีกต่อไป เพราะไม่มีความหมายในทางฟิสิกส์
Okun กล่าวว่าแม้แต่ไอน์สไตน์เอง ก็กล่าวถึงแต่มวลนิ่งในสมการของเขาเ่ท่านั้น(ในสมการของไอน์สไตน์นี้ M คือมวลสัมพัทธ์ m, ส่วน m คือมวลนิ่ง m0 ในความหมายปัจจุบัน)
ดังนั้น Okun เสนอว่าควรพิจารณามวลสัมพัทธ์ผ่านกรอบอนุรักษ์โมเมนตัมมากกว่ามวลสัมพัทธ์ ขณะเดียวกัน Taylor และ Wheeler ต่างก็ยอมรับในแนวคิดนี้คือ "มวลในระบบโดดเดี่ยวมีค่าคงที่" และหลีกเลี่ยงการใช้ relativistic mass เพราะนำไปสู่การเข้าใจผิดได้โดยง่าย
Okun กล่าวว่าแม้แต่ไอน์สไตน์เอง ก็กล่าวถึงแต่มวลนิ่งในสมการของเขาเ่ท่านั้น(ในสมการของไอน์สไตน์นี้ M คือมวลสัมพัทธ์ m, ส่วน m คือมวลนิ่ง m0 ในความหมายปัจจุบัน)
It is not good to introduce the concept of the mass
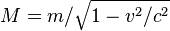
of a moving body for which no clear definition can be given. It is better to introduce no other mass concept than the ’rest mass’ m. Instead of introducing M it is better to mention the expression for the momentum and energy of a body in motion.(Albert Einstein in letter to Lincoln Barnett, 19 June 1948 (quote from L. B. Okun(1989), p. 42)
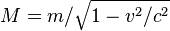
of a moving body for which no clear definition can be given. It is better to introduce no other mass concept than the ’rest mass’ m. Instead of introducing M it is better to mention the expression for the momentum and energy of a body in motion.(Albert Einstein in letter to Lincoln Barnett, 19 June 1948 (quote from L. B. Okun(1989), p. 42)
ดังนั้น Okun เสนอว่าควรพิจารณามวลสัมพัทธ์ผ่านกรอบอนุรักษ์โมเมนตัมมากกว่ามวลสัมพัทธ์ ขณะเดียวกัน Taylor และ Wheeler ต่างก็ยอมรับในแนวคิดนี้คือ "มวลในระบบโดดเดี่ยวมีค่าคงที่" และหลีกเลี่ยงการใช้ relativistic mass เพราะนำไปสู่การเข้าใจผิดได้โดยง่าย
ถึงวันนี้การอภิปรายเรื่องสถานะทางฟิสิกส์ของมวลสัมพัทธ์ ยังเป็นหัวข้อการอภิปรายทางฟิสิกส์ต่อไป แต่มีแนวโน้มยอมรับ "มวลในระบบโดดเดี่ยวมีค่าคงที่"
ตัดเท้าให้เข้ากับเกือก
กรณี การตีความข้างต้น m=m0/0=infinity อุปมาตัดเท่าให้เข้ากับเกือก คือ ลดทอน-จำกัดให้ความจริงทางกายภาพให้น้อยลงโดยอาศัยรากฐานทางคณิตศาสตร์ที่ยังคลุมเครือและมีกรอบจำกัด
กล่าวคือ กรณีหารด้วยศูนย์ ในระบบคณิตศาสตร์มาตรฐาน(Formal operations)บางครั้งดูเหมือนว่าจะมีประโยชน์หากจะคิดว่า a/0 เมื่อ a≠0 จะได้คำตอบเท่ากับ infinity ดังนี้

ขณะเดียวกันจะพบว่า

เมื่อคำตอบของ one-sided limits แต่ละข้างไม่เท่าักัน ดังนั้น 1/0 จึงนิยามไม่ได้ หรือ อนิยาม(undefined)ในระบบ extended real line
นอกจากนี้ข้อความ

จะกลายเป็นข้อความที่ไม่มีความหมาย(meaningless expressions)
อย่างไรก็ตาม ในคณิตศาสตร์บางระบบที่ไม่ใช่คณิตศาสตร์มาตรฐาน เช่น Real projective line อาจกำหนดได้ว่า a/0 = infinity หรือระบบคณิตศาสตร์ Riemann sphere อาจกำหนดได้ว่า a/0=infinity,เมื่อ a ไม่เท่ากับศูนย์
แต่คำตอบนี้, a/0 = infinity, ก็ยังไม่เป็นที่ยอมรับโดยเอกฉันท์ เพราในคณิตศาสตร์แบบ Non-standard analysis เช่น hyperreal numbers และ surreal numbers การหารด้วยศูนย์ก็ยังเป็นไปไม่ได้
นอกจากนี้ในคณิตศาสตร์ชั้นสูงเช่น แคลคูลัส การหารด้วยศูนย์จะชักพาไปสู่ปัญหา ghosts of departed quantities ดังที่ Berkley สร้างขึ้นมาเพื่อวิพากษ์แคลคูลัสของ Newton ส่วนที่เรียกว่า fluxions และวิพากษ์ Leibniz ในส่วนของ infinitesimal change
ใน section 16, Berkeley วิพากษ์ว่า
the fallacious way of proceeding to a certain Point on the Supposition of an Increment, and then at once shifting your Supposition to that of no Increment . . . Since if this second Supposition had been made before the common Division by o, all had vanished at once, and you must have got nothing by your Supposition. Whereas by this Artifice of first dividing, and then changing your Supposition, you retain 1 and nxn-1. But, notwithstanding all this address to cover it, the fallacy is still the same.
และวรรคตอนที่ Berkeley ถูกอ้างถึงบ่อยคือ
And what are these Fluxions? The Velocities of evanescent Increments? And what are these same evanescent Increments? They are neither finite Quantities nor Quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?
ในทัศนะของนักประวัติศาสตร์ความรู้อย่าง Judith Grabiner กล่าวถึง Berkeley ว่า
“Berkeley’s criticisms of the rigor of the calculus were witty, unkind, and—with respect to the mathematical practices he was criticizing—essentially correct”(Grabiner 1997).
สุดท้าย Berkeley แสดงให้เห็นว่า a/0 ไม่มีความหมาย หรือเป็นไปไม่ได้ที่จะหาค่าของมัน เพราะมันจะนำไปสู่ปัญหาความขัดแย้งทางตรรกะ (โปรดู George Berkeley's criticism of infinitesimal calculus in The Analyst; see Ghosts of departed quantities.)
ดังนั้นคำตอบ หรือสถานะของ a/0 ในขณะนี้คือ undefined นั่นคือยังกำหนดไม่ได้ หรือยังไม่กำหนด หรือ ยังไม่นิยาม
อาศัยการตีความตามแคลคูลัสว่า m=m0/0=infinity จึงเป็นการนำคณิตศาสตร์มาอธิบายความจริงทางกายภาพที่เปิดโอกาสให้เกิดความผิดพลาดโดยง่าย
ในเรื่องนี้ m=m0/0=infinity นี้ นักฟิสิกส์ตีความจากกรณีการเร่งอนุภาคให้เท่ากับความเร็วแสงไม่ได้จึงสรุปว่ามวลสัมพัทธ์เป็นอนันต์ แต่ปมปัญหานี้ อาจเกิดจากสาเหตุ 3 ประการ
(1) เทคนิคการเร่งอนุภาคเป็นภาคปฏิบัติ หมายความว่า การที่นักฟิสิกส์เร่งอนุภาคให้เร็วเท่ากับแสงไม่ได้นั้นเป็นปัญหาภาคปฏิบัติ ไม่ใช่ปัญหาเรื่องภาคทฤษฎีที่ว่า v=c แล้วมวลเป็นอนันต์ นั่นคือหากมนุษย์สามารถผลิตเครื่องมือเร่งให้อนุภาคมี v=c ได้ เราอาจจะได้พบต่อไปว่ามวลนิ่งของอนุภาคนั้นจะกลายเป็นศูนย์ นั่นคือมวลในแบบเดิมหายไป(เช่น ในรูปเฟอร์เมียน) แต่กลายเป็นพลังงานจลน์(หรือโมเมนตัม)ทั้งหมด ตามสมการ E=mc2
(2) อนุภาคเมื่อมีความเร็วใกล้แสง จะคายพลังงานที่รับเข้าไปออกมาเสียก่อนที่จะเกิดกรณี v=c เมื่ออนุภาคคายพลังงานออกมา แล้วความเร็วของอนุภาคย่อมลดลง จึงต้องใส่พลังงานเข้าไปเร่งอนุภาคใหม่ อนุภาคจึงมี v=cไม่ได้ ไม่ได้เกิดจากการตีความว่ามวลเป็นอนันต์แต่อย่างใด
ในเรื่องนี้ m=m0/0=infinity นี้ นักฟิสิกส์ตีความจากกรณีการเร่งอนุภาคให้เท่ากับความเร็วแสงไม่ได้จึงสรุปว่ามวลสัมพัทธ์เป็นอนันต์ แต่ปมปัญหานี้ อาจเกิดจากสาเหตุ 3 ประการ
(1) เทคนิคการเร่งอนุภาคเป็นภาคปฏิบัติ หมายความว่า การที่นักฟิสิกส์เร่งอนุภาคให้เร็วเท่ากับแสงไม่ได้นั้นเป็นปัญหาภาคปฏิบัติ ไม่ใช่ปัญหาเรื่องภาคทฤษฎีที่ว่า v=c แล้วมวลเป็นอนันต์ นั่นคือหากมนุษย์สามารถผลิตเครื่องมือเร่งให้อนุภาคมี v=c ได้ เราอาจจะได้พบต่อไปว่ามวลนิ่งของอนุภาคนั้นจะกลายเป็นศูนย์ นั่นคือมวลในแบบเดิมหายไป(เช่น ในรูปเฟอร์เมียน) แต่กลายเป็นพลังงานจลน์(หรือโมเมนตัม)ทั้งหมด ตามสมการ E=mc2
(2) อนุภาคเมื่อมีความเร็วใกล้แสง จะคายพลังงานที่รับเข้าไปออกมาเสียก่อนที่จะเกิดกรณี v=c เมื่ออนุภาคคายพลังงานออกมา แล้วความเร็วของอนุภาคย่อมลดลง จึงต้องใส่พลังงานเข้าไปเร่งอนุภาคใหม่ อนุภาคจึงมี v=cไม่ได้ ไม่ได้เกิดจากการตีความว่ามวลเป็นอนันต์แต่อย่างใด
(3) แนวคิดมวลสัมพัทธ์ มีปัญหาในตัวเอง ซึ่งยังไม่ยุติว่าควรจะพูดถึงมวลสัมพัทธ์ในความหมายใด ดังที่ไอน์สไตน์กล่าวถึงมวลที่เคลื่อนที่ผ่าน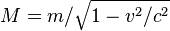 ว่าเป็นแนวคิดที่ไม่ค่อยดีนัก
ว่าเป็นแนวคิดที่ไม่ค่อยดีนัก
(4) มวลสัมพัทธ์ขึ้นอยู่กับกรอบอ้างอิงของผู้วัด(the relativistic mass depends on the observer's frame of reference.)ดังนั้นการที่ผู้วัดได้ตีความภายใต้กฎคณิตศาสตร์ว่า m=infinity จึงเป็นไปไม่ได้ภายใต้กฎอนุรักษ์พลังงานของระบบ(the sum total quantity of energy in a body or system)
อย่างไรก็ตาม ปัญหาใหญ่ของการตีความมวลสัมพัทธ์เป็นอนันต์นี้ ปมปัญหาที่แท้จริงอาจถูกซุกซ่อนอยู่ในความเชื่อมโยงระหว่างคณิตศาสตร์กับฟิสิกส์ ไอน์สไตน์ เคยตั้งข้อห่วงใยไว้ว่า
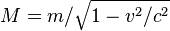 ว่าเป็นแนวคิดที่ไม่ค่อยดีนัก
ว่าเป็นแนวคิดที่ไม่ค่อยดีนัก(4) มวลสัมพัทธ์ขึ้นอยู่กับกรอบอ้างอิงของผู้วัด(the relativistic mass depends on the observer's frame of reference.)ดังนั้นการที่ผู้วัดได้ตีความภายใต้กฎคณิตศาสตร์ว่า m=infinity จึงเป็นไปไม่ได้ภายใต้กฎอนุรักษ์พลังงานของระบบ(the sum total quantity of energy in a body or system)
อย่างไรก็ตาม ปัญหาใหญ่ของการตีความมวลสัมพัทธ์เป็นอนันต์นี้ ปมปัญหาที่แท้จริงอาจถูกซุกซ่อนอยู่ในความเชื่อมโยงระหว่างคณิตศาสตร์กับฟิสิกส์ ไอน์สไตน์ เคยตั้งข้อห่วงใยไว้ว่า
"as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."
กล่าวคือ ความหมายที่ไอน์สไตน์กล่าวถึงอาจตีความได้ดังนี้
(1)ในทางคณิตศาสตร์ ผลจากการ"นิรนัย"จะได้ว่า 50=1, 90=1 ซึ่งในชีวิตจริงเราไม่มีทางคิดเข้าใจได้เลยว่า ข้อความที่แสดงนี้หมายถึงอะไร เกี่ยวข้องกับการบวก ลบ คูณ หารจำนวนซึ่งเป็นพื้นฐานของคณิตศาสตร์อย่างไร? นั่นคือยิ่งเรายอมรับผลจากการนิรนัยว่าเป็นความจริงแน่แท้ คณิตศาสตร์ก็ยิ่งห่างไกลกับความเป็นจริงมากขึ้นทุกที ที่สำคัญกว่านั้นคือการนิรนัยทางคณิตศาสตร์เป็น"การตีความ"ที่มีข้อจำกัดในการสะท้อนความจริงเสมอ
(2) กรณี 3*1 =3 ความหมายพื้นฐานคือ 1 จำนวน 3 ตัวรวมกันได้ 3
ถ้า 1*1=3 ความหมายพื้นฐานคือ 1 จำนวน 1 ตัวรวมกันได้ 1
แล้ว 0*1=0 ความหมายพื้นฐานคือ 1 จำนวน 0 ตัว รวมกันได้ 0 นั่นคือ ไม่มี 1 นั่นเอง ดังนั้นศูนย์ในกรณีการคูณ จึงบอกว่า ไม่มี นั่นเอง
(3) กรณี 3/3 =1 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 3 ได้ผลลัพธ์ 1 ครั้้ง
3/2 = 1+1/2 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 2 ได้ผลลัพธ์ 1 ครั้้ง และเศษอีก 13/4 = 0+3/4 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 4 ได้ผลลัพธ์ 0 ครั้้ง และเศษอีก 3คือตัวตั้ง โดยมีส่วนคือ 4 เท่าเดิม ความหมายผลลัพทธ์ 0 ในที่นี้คือ แบ่งไม่ได้ ไม่ให้แบ่ง คือ ไม่ได้
3/1 =3 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 1 ได้ผลลัพธ์ 3 ครั้้ง
3/0 =1 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 0 ได้ผลลัพธ์ ...?
เทียบจากกรณีการคูณ ที่ความหมายของ 0 ศูนย์ คือ ไม่มี หรือในกรณีการหารเมื่อหารไม่ได้จะได้ผลลัพธ์เป็น 0 ดังนั้น กรณี 3/0 ซึ่งหารไม่ได้ หรือเพราะตัวหารไ่ม่มี คำตอบที่ได้ตามกฎการคูณและการหาร คือ ผลลัพธ์เป็น 0 แล้วบวกกับเศษคือ 3 เขียนในรูปแบบคือ 3/0=0+3/0, และตีความให้อยู่ในรูปเนื้อหา 3/0 =3
นอกจากนี้ในกรณีจุด ซึ่งคณิตศาสตร์ไม่นิยาม หรือเรียกว่า"อนิยาม" เพราะมีลักษณะของ circularity แต่โดยทั่วไปนักคณิตศาสตร์กล่าวถึงจุดตำแหน่งของจำนวนเต็มบนเส้นจำนวน เช่น 5 ราวกับว่ามันมีอยู่จริง และจำนวนที่มากที่สุดแต่น้อยกว่า 5 คือ 4.999... ทั้งที่จุดที่ 5 ตั้งอยู่ไม่มีอยู่จริง
(1)ในทางคณิตศาสตร์ ผลจากการ"นิรนัย"จะได้ว่า 50=1, 90=1 ซึ่งในชีวิตจริงเราไม่มีทางคิดเข้าใจได้เลยว่า ข้อความที่แสดงนี้หมายถึงอะไร เกี่ยวข้องกับการบวก ลบ คูณ หารจำนวนซึ่งเป็นพื้นฐานของคณิตศาสตร์อย่างไร? นั่นคือยิ่งเรายอมรับผลจากการนิรนัยว่าเป็นความจริงแน่แท้ คณิตศาสตร์ก็ยิ่งห่างไกลกับความเป็นจริงมากขึ้นทุกที ที่สำคัญกว่านั้นคือการนิรนัยทางคณิตศาสตร์เป็น"การตีความ"ที่มีข้อจำกัดในการสะท้อนความจริงเสมอ
(2) กรณี 3*1 =3 ความหมายพื้นฐานคือ 1 จำนวน 3 ตัวรวมกันได้ 3
ถ้า 1*1=3 ความหมายพื้นฐานคือ 1 จำนวน 1 ตัวรวมกันได้ 1
แล้ว 0*1=0 ความหมายพื้นฐานคือ 1 จำนวน 0 ตัว รวมกันได้ 0 นั่นคือ ไม่มี 1 นั่นเอง ดังนั้นศูนย์ในกรณีการคูณ จึงบอกว่า ไม่มี นั่นเอง
(3) กรณี 3/3 =1 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 3 ได้ผลลัพธ์ 1 ครั้้ง
3/2 = 1+1/2 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 2 ได้ผลลัพธ์ 1 ครั้้ง และเศษอีก 13/4 = 0+3/4 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 4 ได้ผลลัพธ์ 0 ครั้้ง และเศษอีก 3คือตัวตั้ง โดยมีส่วนคือ 4 เท่าเดิม ความหมายผลลัพทธ์ 0 ในที่นี้คือ แบ่งไม่ได้ ไม่ให้แบ่ง คือ ไม่ได้
3/1 =3 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 1 ได้ผลลัพธ์ 3 ครั้้ง
3/0 =1 ความหมายพื้นฐานคือ 3 แบ่งครั้งละ 0 ได้ผลลัพธ์ ...?
เทียบจากกรณีการคูณ ที่ความหมายของ 0 ศูนย์ คือ ไม่มี หรือในกรณีการหารเมื่อหารไม่ได้จะได้ผลลัพธ์เป็น 0 ดังนั้น กรณี 3/0 ซึ่งหารไม่ได้ หรือเพราะตัวหารไ่ม่มี คำตอบที่ได้ตามกฎการคูณและการหาร คือ ผลลัพธ์เป็น 0 แล้วบวกกับเศษคือ 3 เขียนในรูปแบบคือ 3/0=0+3/0, และตีความให้อยู่ในรูปเนื้อหา 3/0 =3
นอกจากนี้ในกรณีจุด ซึ่งคณิตศาสตร์ไม่นิยาม หรือเรียกว่า"อนิยาม" เพราะมีลักษณะของ circularity แต่โดยทั่วไปนักคณิตศาสตร์กล่าวถึงจุดตำแหน่งของจำนวนเต็มบนเส้นจำนวน เช่น 5 ราวกับว่ามันมีอยู่จริง และจำนวนที่มากที่สุดแต่น้อยกว่า 5 คือ 4.999... ทั้งที่จุดที่ 5 ตั้งอยู่ไม่มีอยู่จริง
แม้กระทั่งจุดที่เรียกว่า"ศูนย์" บนเส้นจำนวน จริงๆแล้วไม่มี เพราะจุดนั้นเป็น"อนิยาม"มาแต่แรก
ดังนั้นการคาดหวังว่าระบบคณิตศาสตร์ปัจจุบันที่รากฐานมาจาก"อนิยาม" ว่ามันสามารถให้คำตอบได้ทุกกรณีนั้น จึงเป็นการฝากความหวังกับสิ่งที่พิการมากเกินไป
ดังนั้นการคาดหวังว่าระบบคณิตศาสตร์ปัจจุบันที่รากฐานมาจาก"อนิยาม" ว่ามันสามารถให้คำตอบได้ทุกกรณีนั้น จึงเป็นการฝากความหวังกับสิ่งที่พิการมากเกินไป
เพราะเมื่อคณิตศาสตร์ต้องเผชิญปัญหาจากสิ่งที่เรียกว่า"ความต่อเนื่อง"(โปรดอ่านเพิ่มเติม)โดยเริ่มต้นจาก"จุด"ซึ่งเป็นวัตถุแห่งการคิดที่มีปัญหามาแต่เริ่มต้นเพราะนิยามไม่ได้ และจากจุดนี้ได้ชักพานักคณิตศาสตร์ไปสู่ปัญหาใหญ่อื่นๆตามมา เช่น ตำแหน่งที่ตั้งของ"จำนวนนับ"บนเส้นจำนวน กรณีหารด้วยศูนย์ หรือกรณีต้องอธิบายปัญหาของเซโนแห่งอีเลียเรื่อง การเคลื่อนที่เป็นมายา รวมถึงปัญหา a/0 เป็นต้น
ดังนั้นสิ่งที่ระบอบคณิตศาสตร์ปัจจุบันมอบให้ฟิสิกส์ คือความจริงที่ถูกลดทอนที่เกิดจากการนิยาม อนิยาม และนิรนัย โดยสารัตถะของคณิตศาสตร์คือข้อจำกัดของความจริง และความจริงของคณิตศาสตร์นี้ไปลดทอน"สัจจะ"ทางกายภาพของฟิสิกส์ในที่สุด
นั่นคือ เราอาจถูกคณิตศาสตร์ลวง หรือล่อให้ติดกับดักได้โดยง่าย เพราะรากฐานของคณิตศาสตร์เริ่มจากสิ่งที่เรียกว่าอนิยาม เช่น จุดบนเส้นจำนวน เส้นตรง และระนาบ
ดังนั้น การตีความฟิสิกส์ผ่านระบบคณิตศาสตร์ในปัจจุบัน จึงเปิดโอกาสให้เกิดความสุ่มเสี่ยงต่อการตัดเท้าให้เข้ากับเกือก คือ การลดทอนความจริงทางฟิสิกส์ให้เหลือเท่ากับกฎเกณ์ทางคณิตศาสตร์ ซึ่งคณิตศาสตร์ยังมีข้อจำกัดในการอธิบายเรื่อง การเปลี่ยนแปลงเชิงคุณภาพ หรือ การเปลี่ยนสถานะของสสาร
เช่น H+H = 2H ตามสมการนี้คือ ธาตุไฮโดรเจน"เหมือนกัน"ทุกประการ จำนวน 2อะตอม รวมกันได้ธาตุไฮโดรเจน2ตัว หรือว่า สิ่งที่คณิตศาสตร์ละเลย มองข้าม หรือไม่อธิบาย คือ มีการเกิดคุณภาพใหม่ ที่ไม่เหมือนอะตอมไฮโดรเจนเิดิมอีกต่อไป
หารด้วยศูนย์ มีความหมายทางฟิสิกส์?
กรณีแฝดคู่ หรือ twin paradox การตีความกรณีที่อนุภาคเคลื่อนที่ความเร็วเท่าแสง ผู้สังเกตที่อยู่ในอนุภาค-ยานอวกาศนั้นจะพบว่าเวลาที่เปลี่ยนแปลงเท่ากับศูนย์ นั่นคือ ไม่มีเวลาในกรอบการเคลื่อนที่นั้น ขณะเดียวกันผู้สังเกตุที่อยู่ในกรอบอ้างอิงคงที่จะพบว่าเวลาที่วัดได้เท่ากับ อินฟินิตี้?
คณิตศาสตร์กำลังลวงหรือบอก?
กล่าวอธิบายในภาษาทั่วไปคือ ผู้ที่เดินทางด้วยความเร็วเท่าแสงจะไม่แก่ ขณะที่ผู้สังเกตในกรอบอ้างอิงที่ไม่มีอัตราเร่ง จะพบว่าผู้นั้นเป็นอมตะนิรันดร์ ดังนั้นการตีความคณิตศาสตร์กรณีเท่ากับอินฟินิตี้ จึงมีความหมายทางฟิสิกส์ว่า"สิ่งนั้นอมตะ"ก็ได้
กรณีมวลสัมพัทธ์ของอนุภาคขณะมีความเร็วเท่ากับแสง อธิบายได้ดังนี้
คณิตศาสตร์กำลังลวงหรือบอก?
กล่าวอธิบายในภาษาทั่วไปคือ ผู้ที่เดินทางด้วยความเร็วเท่าแสงจะไม่แก่ ขณะที่ผู้สังเกตในกรอบอ้างอิงที่ไม่มีอัตราเร่ง จะพบว่าผู้นั้นเป็นอมตะนิรันดร์ ดังนั้นการตีความคณิตศาสตร์กรณีเท่ากับอินฟินิตี้ จึงมีความหมายทางฟิสิกส์ว่า"สิ่งนั้นอมตะ"ก็ได้
กรณีมวลสัมพัทธ์ของอนุภาคขณะมีความเร็วเท่ากับแสง อธิบายได้ดังนี้
m=m0+E นั่นคือ มวลสัมพัทธ์ จะมีค่าเท่ากับ มวลนิ่ง+พลังงานจลน์ที่เพิ่มขึ้นเพราะความเร็วที่เพิ่มขึ้น
นั่นคือ ความเร็วที่เพิ่มขึ้นทำให้วัตถุนั้นมีพลังงานเพิ่มขึ้น มีโมเมนตัมเพิ่มขึ้น ขณะเดียวกันมวลนิ่งยังมีค่าเท่าเดิม ส่วนที่เพิ่มมาคือ พลังงานจลน์ หรือ โมเมนตัมเท่านั้น
จากการทดลองในเรื่อง two-photons physics พบว่าอนุภาคที่มีประจุ เช่น อิเลคตรอน เมื่อถูกเร่งให้มีความเร็วใกล้แสงผ่านเครื่อง synchroton จะเกิด synchrotron radiation โดยอนุภาคจะแผ่รังสีแกมมา หรืออนุภาคโฟตอนออกมา หมายความว่า ณ ความเร็วใกล้แสง ทำให้อนุภาคที่มีประจุ(และอื่นๆ)จะประพฤติตัวไปในทิศทางรูปแบบของแสง(คลื่นแม่เหล็กไฟฟ้า) และก่อนที่อนุภาคจะไปถึง v=c ได้ อนุภาคเหล่านั้นจะปลดปล่อยพลังงานออกมาเสียก่อน ดังนั้นในทางปฏิบัติ นักฟิสิกส์จึงไม่อาจเร่งให้อนุภาคเดินทางเร็ว v=c ได้ แต่อาจมีหนทางอื่น?
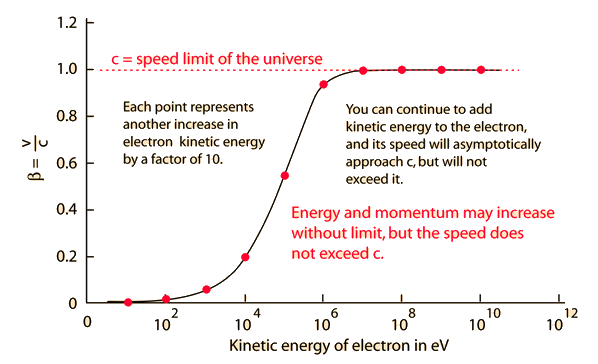 source:http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
source:http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.htmlจากกราฟที่ยกมาแสดงนี้ จะเห็นว่าอิเลคตรอนจะมีพลังงานจลน์ได้ไม่จำกัด ขณะที่ความเร็วของอิเลคตรอนจะถูกจำกัดไว้ กล่าวคือ อิเลคตรอนจะวิ่งด้วยความเร็วแสงไม่ได้ กราฟนี้ขัดแย้งกับข้อเท็จจริงที่ว่าอนุภาคที่เคลื่อนที่ด้วยความเร็วใกล้แสงจะปลดปล่อยคายโฟตอนออกมา ดังนั้นเมื่อพลังงานที่เพิ่มเข้าไปให้อนุภาค แต่อนุภาคคายออกมา ด้วยเหตุนี้ในทางทฤษฎีและปฏิบัติจึงไม่อาจเร่งอนุภาคให้เร็วเท่าแสงได้
ดังนั้น กรณีอนุภาคมี v=c , แล้ว m=m0/0 =infinity มีความหมายมากกว่าการตีความเถรตรงผ่านคณิตศาสตร์ว่ามวลอนันต์ อย่างน้อยก็มีนัยความหมาย ดังนี้
(1) ใช้พลังงานจำนวนอนันต์หรือทั้งจักรวาล ก็เร่งอนุภาคนั้นให้เร็วเท่าแสงไม่ได้ เพราะอนุภาคนั้นคายพลังงานออกมาก่อนที่ความเร็ว v=c
(2) การหารด้วยศูนย์ ในกรณีนี้ผู้สังเกตในกรอบที่ไม่มีอัตราเร่ง จะพบว่าอนุภาคนั้นหายไป คือมวลนิ่งเป็นศูนย์ แล้วมวลทั้งหมดอยู่ในรูปพลังงานจลน์เท่านั้น
ตัวอย่างการคำนวณเช่น หาโมเมนตัมสัมพัทธ์และพลังงานสัมพัทธ์ของอิเลคตรอน 1 ตัว ที่ v=0.99c
จากสมการ
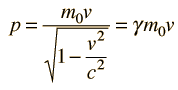
แทนค่า v= 0.99c จะได้ p= 1.9165915387064862*10^-21 kg.m/s
หรือคำนวณหาพลังงานสัมพัทธ์ของอิเลคตรอน จากสมการ
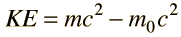
หรือ E=mc2= m0c2+KE
ที่ v=0.99c มวลนิ่งอิเลคตรอน เป็นไปตามสมการ E=m0c2= 9.109*10^-31*(2.99792*108)^2= 8.18673590891776*10^-14 joule หรือ 0.511 MeV เมื่อ 1eV=1.602176487*10-19J
E= mc2 =γm0c2 = 7.0888*9.109*10^-31*(2.99792*10^8)^2 =58.034*10^-14 joule=3.622 MeV
KE=mc2-m0c2= 3.622-0.511=3.11
ดังนั้น พลังงานสัมพัทธ์ E ของอิเลคตรอนที่ v=0.99c เ็ป็นไปตามสมการ E= m0c2+KE=0.511+ 3.11 =3.621 MeV
หรือ คำนวณพลังงานสัมพัทธ์จาก E2 = p2c2+m02c4 เมื่อ p= 1.91659*10^-21 kg.m/s ก็ได้
หรือคำนวณหาพลังงานสัมพัทธ์ของอิเลคตรอน จากสมการ
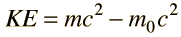
หรือ E=mc2= m0c2+KE
ที่ v=0.99c มวลนิ่งอิเลคตรอน เป็นไปตามสมการ E=m0c2= 9.109*10^-31*(2.99792*108)^2= 8.18673590891776*10^-14 joule หรือ 0.511 MeV เมื่อ 1eV=1.602176487*10-19J
E= mc2 =γm0c2 = 7.0888*9.109*10^-31*(2.99792*10^8)^2 =58.034*10^-14 joule=3.622 MeV
KE=mc2-m0c2= 3.622-0.511=3.11
ดังนั้น พลังงานสัมพัทธ์ E ของอิเลคตรอนที่ v=0.99c เ็ป็นไปตามสมการ E= m0c2+KE=0.511+ 3.11 =3.621 MeV
หรือ คำนวณพลังงานสัมพัทธ์จาก E2 = p2c2+m02c4 เมื่อ p= 1.91659*10^-21 kg.m/s ก็ได้
ดังนั้นภายใต้ปรากฏการณ์การเร่งอนุภาคหรือ Synchrotron radiation พยากรณ์ต่อไปได้ว่าหาก อิเลคตรอนถูกเร่งให้มีควมเร็วเท่ากับแสง(ในอุดมคติ) ผู้สังเกตุจะพบว่าอิเลคตรอนในรูปสสาร(matter)เดิมนั้น จะต้องเลือนหายไป กล่าวคือ คือมวลนิ่งในความหมายเดิม หรือรูปแบบสสารเดิมหายไป กลายเป็นสิ่งใหม?
แต่เนื่องจากคุณสมบัติของแสงซึ่งเป็นคลื่นแม่เหล็กไฟฟ้าและโฟตอนขณะเดียวกัน บ่งชี้ว่าสิ่งที่เคลื่อนที่ด้วยความเร็วแสง จะมีมวลนิ่งเป็นศูนย์ หมายความต่อไปว่าว่าอนุภาคที่ v=c จะมีมวลนิ่งเป็นศูนย์ด้วย
ดังนั้น m=m0+E จึงเขียนใหม่ได้ว่า m=0+E=E นั่นคือ วัตถุนั้นมีพลังงานสัมพัทธ์ E=mc2= m0c2+KE หรือ E2 = p2c2+m02c4 นั่นเอง
ตีความ m=0+E เมื่อ m0=m/γ
กรณีวัตถุใดเคลื่อนที่ด้วยความเร็วเท่าแสง มวลสัมพัทธ์ควรจะเป็นอย่างไร?
ในปี 1934 Tolman ได้นิยามมวลสัมพัทธ์สำหรับทุกอนุภาคที่มี v=c ว่า m=E/c2
(for all particles, including those moving at the speed of light)
โดยเฉพาะอย่างยิ่ง กรณีเวลาในกรอบของอนุภาคที่เคลื่อนที่ v=c นักฟิสิกส์จะตีความว่าเวลาในกรอบของอนุภาคจะเท่ากับศูนย์ ขณะที่เวลาในกรอบของผู้สังเกตุจะเท่ากับอนันต์
ขณะเดียวกันที่ v=c ตามทฤษฎีสัมพัทธภาพพิเศษนั้น ความยาววัดได้จะหดสั้นกลายเป็นศูนย์(โปรดดูการคำนวณ) นั่นคือ ผู้สังเกตุจะมองไม่เห็นขนาดหรือความยาวของอนุภาคหรือวัตถุนั้นอีกต่อไป
ดังนั้นถ้าความยาวของอนุภาคหรือวัตถุนั้นมีความยาวเท่ากับศูนย์ หรือหายไปจากสายตาของผู้สังเกตุ แล้วมวลนิ่งของวัตถุนั้นจะมีสภาพการณ์เป็นอย่างไร?
(1) ตีความผ่านมวลนิ่ง เนื่องจากการคำนวณผ่านกรอบคณิตศาสตร์ำ ขณะที่ v=c ทำให้มวลสัมพัทธ์กลายเป็นอนันต์ ดังนั้นหากมองมุมกลับ คือย้อนไปดูสถานะของมวลนิ่งขณะ v=c ว่ามวลนิ่งมีคุณสมบัติรูปร่างเป็นอย่างไร? จะพบว่าเป็นดังนี้ จาก m=γm0, m0=m/γ,
ในปี 1934 Tolman ได้นิยามมวลสัมพัทธ์สำหรับทุกอนุภาคที่มี v=c ว่า m=E/c2
(for all particles, including those moving at the speed of light)
โดยเฉพาะอย่างยิ่ง กรณีเวลาในกรอบของอนุภาคที่เคลื่อนที่ v=c นักฟิสิกส์จะตีความว่าเวลาในกรอบของอนุภาคจะเท่ากับศูนย์ ขณะที่เวลาในกรอบของผู้สังเกตุจะเท่ากับอนันต์
ขณะเดียวกันที่ v=c ตามทฤษฎีสัมพัทธภาพพิเศษนั้น ความยาววัดได้จะหดสั้นกลายเป็นศูนย์(โปรดดูการคำนวณ) นั่นคือ ผู้สังเกตุจะมองไม่เห็นขนาดหรือความยาวของอนุภาคหรือวัตถุนั้นอีกต่อไป
ดังนั้นถ้าความยาวของอนุภาคหรือวัตถุนั้นมีความยาวเท่ากับศูนย์ หรือหายไปจากสายตาของผู้สังเกตุ แล้วมวลนิ่งของวัตถุนั้นจะมีสภาพการณ์เป็นอย่างไร?
(1) ตีความผ่านมวลนิ่ง เนื่องจากการคำนวณผ่านกรอบคณิตศาสตร์ำ ขณะที่ v=c ทำให้มวลสัมพัทธ์กลายเป็นอนันต์ ดังนั้นหากมองมุมกลับ คือย้อนไปดูสถานะของมวลนิ่งขณะ v=c ว่ามวลนิ่งมีคุณสมบัติรูปร่างเป็นอย่างไร? จะพบว่าเป็นดังนี้ จาก m=γm0, m0=m/γ,
เมื่อ v=c, ดังนั้น γ=0 แต่เนื่องจาก m/γ ก็คือ m*0
ดังนั้น m0=m/γ=0
หมายความว่า อนุภาคที่ v=c ทำให้ มวลนิ่งกลายเป็นศูนย์, m0=0, นั่นคือ ผู้สังเกตุจะพบว่า อนุภาคนั้นวัดไม่ได้ในแบบเดิมอีกต่อไป แต่เนื่องจากมวลและพลังงานในระบบเป็นสิ่งคงที่ เมื่อมวลนิ่งหายไป แสดงว่ามวลต้องเปลี่ยนรูปไปอยู่ในรูปแบบอื่น เช่น โมเมนตัม หรือพลังงาน
ขณะเดียวกัน มวลของอนุภาคที่ v=c เป็นไปตามสมการ E=mc2 ด้งนั้น"พยากรณ์"ได้ว่าอนุภาคนั้นจะประพฤติตนเป็นแสง คือ มีมวลนิ่งเป็นศูนย์ และมีพลังงานที่ขึ้นอยู่กับโมเมนตัม หรือความถี่
(2) ตีความ m=m0/0 = บางสิ่ง = วัตถุนั้นหายไป=มีมวลนิ่งเป็นศูนย์ตามข้อ(1) พยากรณ์ได้ว่าจะเกิดการเปลี่ยนสถานะทางสสารกลายเป็นสสารใหม่แต่มีมวลเท่าเดิม ภายให้หลักสมมูลที่ว่า"มวลคือพลังงานและพลังงานคือมวล" นั่นคือ มวลนิ่งในความหมายเดิมที่เคยวัดได้จะกลายเป็นศูนย์ โดยมวลนิ่งจะเปลี่ยนเป็นคลื่นแม่เหล็กไฟ้ฟ้าแทน
การตีความแบบนี้ สอดรับกับกรณีการหารด้วยศูนย์อย่างไร?
ดังนั้น m0=m/γ=0
หมายความว่า อนุภาคที่ v=c ทำให้ มวลนิ่งกลายเป็นศูนย์, m0=0, นั่นคือ ผู้สังเกตุจะพบว่า อนุภาคนั้นวัดไม่ได้ในแบบเดิมอีกต่อไป แต่เนื่องจากมวลและพลังงานในระบบเป็นสิ่งคงที่ เมื่อมวลนิ่งหายไป แสดงว่ามวลต้องเปลี่ยนรูปไปอยู่ในรูปแบบอื่น เช่น โมเมนตัม หรือพลังงาน
ขณะเดียวกัน มวลของอนุภาคที่ v=c เป็นไปตามสมการ E=mc2 ด้งนั้น"พยากรณ์"ได้ว่าอนุภาคนั้นจะประพฤติตนเป็นแสง คือ มีมวลนิ่งเป็นศูนย์ และมีพลังงานที่ขึ้นอยู่กับโมเมนตัม หรือความถี่
(2) ตีความ m=m0/0 = บางสิ่ง = วัตถุนั้นหายไป=มีมวลนิ่งเป็นศูนย์ตามข้อ(1) พยากรณ์ได้ว่าจะเกิดการเปลี่ยนสถานะทางสสารกลายเป็นสสารใหม่แต่มีมวลเท่าเดิม ภายให้หลักสมมูลที่ว่า"มวลคือพลังงานและพลังงานคือมวล" นั่นคือ มวลนิ่งในความหมายเดิมที่เคยวัดได้จะกลายเป็นศูนย์ โดยมวลนิ่งจะเปลี่ยนเป็นคลื่นแม่เหล็กไฟ้ฟ้าแทน
การตีความแบบนี้ สอดรับกับกรณีการหารด้วยศูนย์อย่างไร?
พิจารณาโจทย์ a/0 = ? อาศัยแนวคิดพื้นฐานการคูณและการหารดังได้กล่ามาแล้วในหัวข้อที่ผ่านมา
จะได้ว่า a/0 =0+a/0 แบ่งพิจารณาได้ 2 กรณี ผลลัพธ์และเศษ ดังนี้
(1) ผลลัพธ์ 0 มีความหมายบ่งชี้ว่า สิ่งนั้นไม่มี หรือ"หายไป" แล้วได้เศษที่เท่ากับตัวตั้ง(โปรดอ่านเพิ่มเติมกรณีหารด้วยศูนย์ใน http://pudalay7000.blogspot.com/2009/03/a0ba.html)
(2) เศษ a/0 พิจารณาได้ดังนี้
(2) เศษ a/0 พิจารณาได้ดังนี้
(2.1) ในเชิงรูปแบบ "นิยาม" ได้ว่า a/0=0+a/0 , พิสูจน์...ผลลัพธ์ 0+เศษ a และส่วนคือ 0 = a/0(เปรียบเทียบกรณี "นิยาม" 5^0=1เป็นผลจากการนิรนัย ที่อาจไม่มีความจริงทางกายภาพรองรับ)
(2.2) ในเชิงเนื้อหา"นิยาม"ได้ว่า a/0 คือ a หรือตัวของมันเอง
แนวคิดหารด้วยศูนย์นี้ มหาวีระ นักปรัชญาชาวอินเดีย เคยกล่าวไว้ในปี ค.ศ. 830 หนังสือชื่อ Ganita Sara Samgraha: ว่า "a number remains unchanged when divided by zero."
การหารด้วยศูนย์ เราอาจยังค้นไม่พบประโยชน์ในกรณีทั่วไป แต่กรณีวัตถุเปลี่ยนสถานะ เพราะเหตุแห่งการเคลื่อนที่ด้วยความเร็วแสง การหารด้วยศูนย์จะช่วยอธิบายให้เห็นภาพการเปลี่ยนแปลงทาง"โครงสร้างภายในของสสาร"ได้อย่างชัดเจน
สรุป ข้อเสนอเชิงทฤษฎี
(1) วัตถุหรือสสารใดที่เคลื่อนที่ด้วยความเร็วแสง v=c สิ่งนั้นจะต้องมี"สภาพ"เป็นคลื่นแม่เหล็กไฟฟ้า
(2) มวลนิ่งของวัตถุตามข้อ(1) ที่ v=c จะกลายเป็นศูนย์
(3) ที่ v=c มวลของวัตถุนั้นทั้งหมด จะกลายเป็นพลังงานจลน์ ตามสมการ E2 = p2c2+m02c4 เมื่อ m0 คือมวลนิ่งของวัตถุนั้น
(4) รูปแบบของสสารจะสัมพันธ์กับความเร็ว อนุภาคเฟอร์เมียน v<c, คลื่นแม่เหล็กไฟฟ้า v=c, เตคีออน v>c
(5) การหารด้วยศูนย์ (5.1)เชิงรูปแบบ"นิยาม"ได้ว่า a/0=0+a/0 (5.2)เชิงเนื้อหา"นิยาม"ได้ว่า a/0=a หรือเท่ากับตัวมันเอง
(6) การหารด้วยศูนย์ ใช้อธบายในกรณีที่คณิตศาสตร์ต้องเกี่ยวเนื่องกับการเปลี่ยนแปลงเชิงคุณภาพได้ เช่น เปลี่ยนรูปแบบของสสารจากสิ่งหนึ่งไปเป็นอีกสิ่งหนึ่ง แต่กรณีทั่วไปนั้น การหารด้วยศูนย์จะมีค่าเท่ากับอนันต์
ป.ล.จะทยอยแก้ไข-เพิ่มเติมบทความนี้ มีเชิงอรรถ บรรณานุกรมตามเวลาที่พอมีและสะดวก ขอบคุณทุกท่านที่ร่วมแบ่งปันและวิจารณ์

ไม่มีความคิดเห็น:
แสดงความคิดเห็น